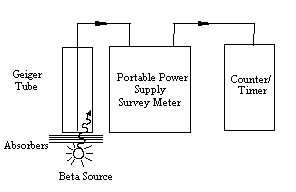
Equipment: Geiger detector, beta sources, set of foils, simple platform to support foils, scaler.
Readings: Interactions of charged particles, 5.2.2 and 5.2.6; Geiger detectors, sect. 5.3.1; Range measurements, sect. 5.4.3.
Key concepts: Energy loss of a charged particle, and its range; range versus energy; different sources of background counting rates.
Sources are available that emit essentially only beta rays (e.g. see
table below). Choosing at least three sources with a range of maximum beta
energies, make measurements of the numbers of betas transmitted through
stacks of Al foils of varying thickness and detected in the Geiger counter.
You will need ~100 small sheets of standard kitchen Al foil (e.g., "Reynold's
Warp"), which are usually quite close to ~0.001" thick. Determine
the counting rate as a function of absorber thickness. The challenge
in this experiment is to determine the thickness for which all beta-rays
are stopped. Obtain statistically significant measurements of rates
for thicknesses in the range where the "true" transmitted counting rate
has dropped to about 1/10 of the background rate. Note that
this may imply lengthy mesurements. By "background" is indicated
a counting rate that remains constant for thick absorbers over the range
of foil thicknesses studied. After subtracting "background" from
your raw data, plot the transmitted counts versus Al thickness on semi-log
paper (as illustrated in fig. 5.32 in Melissinos). Indicate the background
level on your plot. Draw error bars for each datum that reflect random
counting errors and propagated errors from background subtraction. Draw
a smooth curve through the data "to guide the eye" and make your best estimate
of the range of betas for each source (with experimental uncertainty) in
units of mg/cm2 of Al. The table gives the maximum energies
of betas for sources that may be available.
| Beta sources | Max. kinetic energy (MeV) |
| 14C | 0.155 |
| 99Tc | 0.29 |
| 36Cl | 0.715 |
| 204Tl | 0.763 |
| 210Bi | 1.17 |
| 234Pa | 2.32 |
3.2 Beta range in other absorbers
Make range measurements using sheets or thicknesses of another absorber such as plastic film. Determine the range in mg/cm2 as in part 3.1 above. Compare the ranges in Al and the other absorber. Try to explain any differences using a simple model to describe the energy loss of electrions in the different materials. .
3.3 Range-energy relation
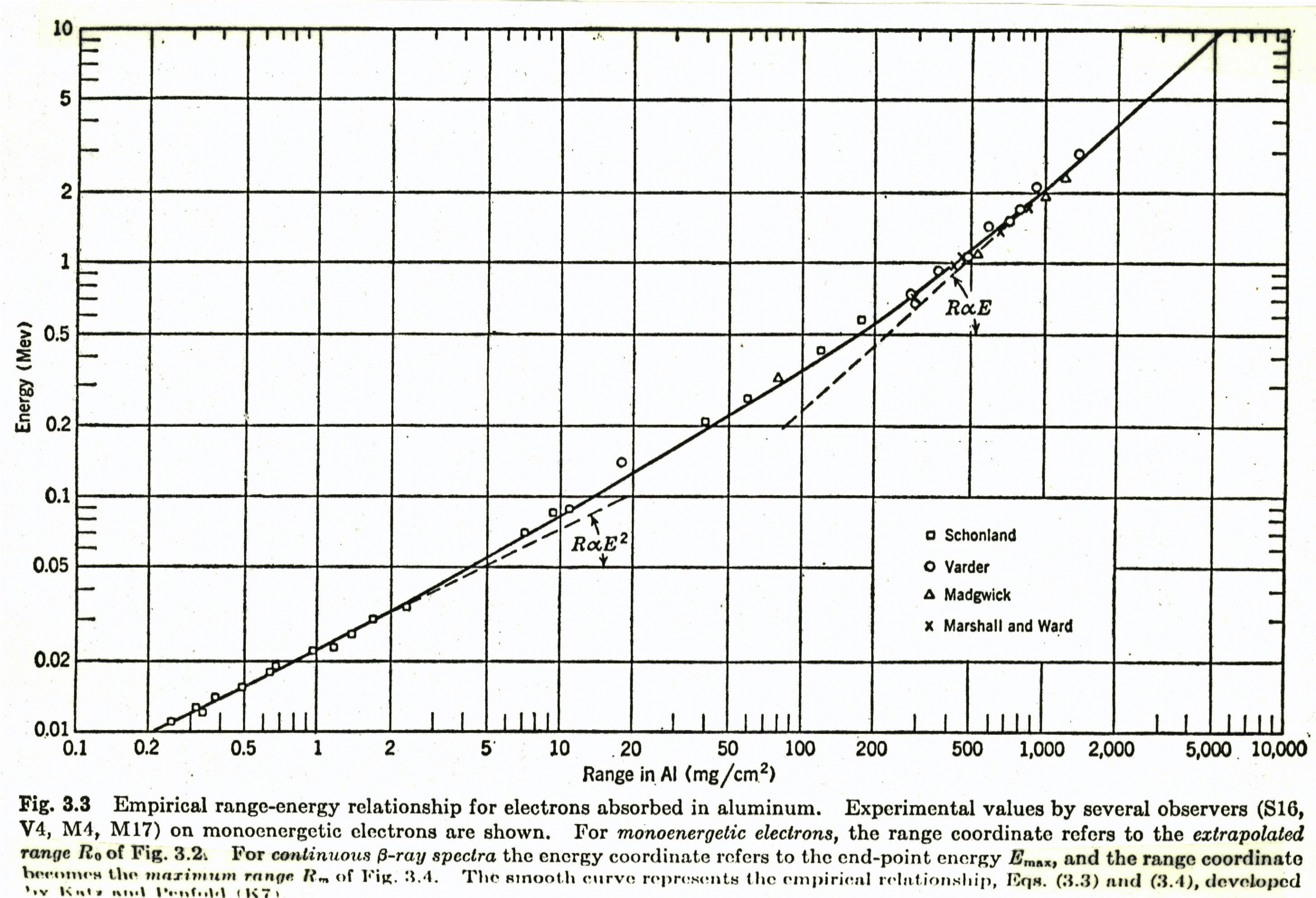
Correct your measured ranges for the energy-loss of betas in the air between source and detector and in the thin mica window of the Geiger counter (thickness ~2.0 mg/cm2). Plot corrected ranges versus maximum beta energy. Compare your values with Feather's formula (eq. 5.2.13) or with the range-energy plot given below. .
3.4 Crude determination of the beta spectrum
Assuming that the energy-loss per unit thickness of absorber is independent of energy, the derivative of the transmitted counting rate with respect to absorber thickness should yield the energy spectrum of the source. Make a plot of the beta spectrum by taking the derivative of your background corrected counting rates. While the result is more qualitative than quantitative, you should be able to demonstrate the broad, continuous nature of the beta-spectrum. (More precise measurements of the energy spectrum can be obtained using a magnetic spectrometer or semiconductor detector such as the high-purity Ge detector used in th high resolution spectroscopy lab.)
a. Enumerate possible sources of "background" counting rates. Consider different types of radiation and their penetrating ability. Also consider if any background might be attributable to the source. What empirical method might you use to determine the background? Could Bremsstrahlung play a role?
b. Consider how best to plan your measurement times in order to obtain the most precise values of the background-corrected counting rates.
c. Beta ranges, when expressed in units of mg/cm2, are experimentally found to be approximately the same for different absorbers. What is the theoretical justification for this trend?
d. 137Cs undergoes beta decay to an excited state of 137Ba, which in turn decays to the ground state of 137Ba with emission of a 0.662 MeV gamma ray. Is it possible to determine the range of betas emitted from 137Cs by the method used in this experiment? Give an argument or (better) try it.