Robert Lorbeski
EM 595 Application of Constraints Management
The Dice Game
The purpose of the dice game is to gain a sense for how a chain of dependent activities, events, or manufacturing steps is affected by the performance of individual elements of the chain. Each element or step in the chain is capable of producing a varying number of products for each iteration of the cycle. Steps in the process consume products from the preceding steps, so the full capability can be used only if the proceeding step has provided sufficient product. Since there is variation in the output steps, there may not be sufficient products to consume in following steps. This will limit the throughput of the system.
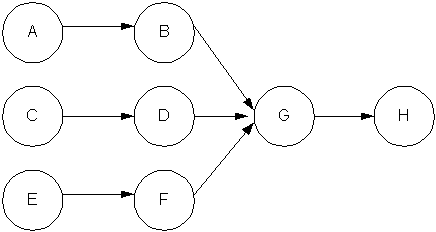
Below is a depiction of a simple three-branch system. In this system, all steps are capable of producing from 1 to 6 parts. Nodes A, C, and E produce detail parts. Nodes B, D, and F use the detail parts from the preceding step and supply subassemblies to node G. G requires 1B, 1D, and 1F part to create its assembly. H uses the assembly produced in G.
The following table contains the data collected during the dice game. The game was played for 10 iterations. Values in the cells of the table represent the capability and throughput for a node. Throughput is shown as a parenthetical value when it is less than the capability.
|
Iteration/Node |
A |
B |
C |
D |
E |
F |
G |
H |
|
1 |
4 |
3 |
2 |
4 (2) |
5 |
6 (5) |
5 (2) |
2 |
|
2 |
3 |
1 |
4 |
4 |
6 |
2 |
1 |
2 (1) |
|
3 |
1 |
6 (4) |
4 |
5 (4) |
4 |
1 |
2 |
4 (2) |
|
4 |
6 |
4 |
3 |
6 (3) |
1 |
5 |
1 |
5 (1) |
|
5 |
4 |
3 |
2 |
6 (2) |
6 |
5 |
5 |
2 |
|
6 |
6 |
1 |
6 |
6 |
6 |
3 |
5 |
6 |
|
7 |
3 |
4 |
6 |
2 |
1 |
1 |
6 (4) |
2 |
|
8 |
5 |
2 |
6 |
2 |
4 |
6 |
2 |
5 |
|
9 |
2 |
3 |
3 |
6 |
2 |
2 |
3 |
6 (4) |
|
10 |
4 |
6 |
2 |
6 |
1 |
6 |
2 |
1 |
|
Total |
38 |
33 (31) |
38 |
47 (37) |
36 |
37 (36) |
33 (27) |
35 (26) |
|
Work in progress |
7 |
4 |
1 |
10 |
0 |
9 |
1 |
0 |
From the results, it is evident that the throughput of the system is limited by performance of prior steps. The overall output of the system is less than the average expected value. 50 process steps were dependent on products from a prior step, insufficient products limited 12 of the steps. Work in progress was unevenly scattered through the process and ranged from 0 to 10 parts.
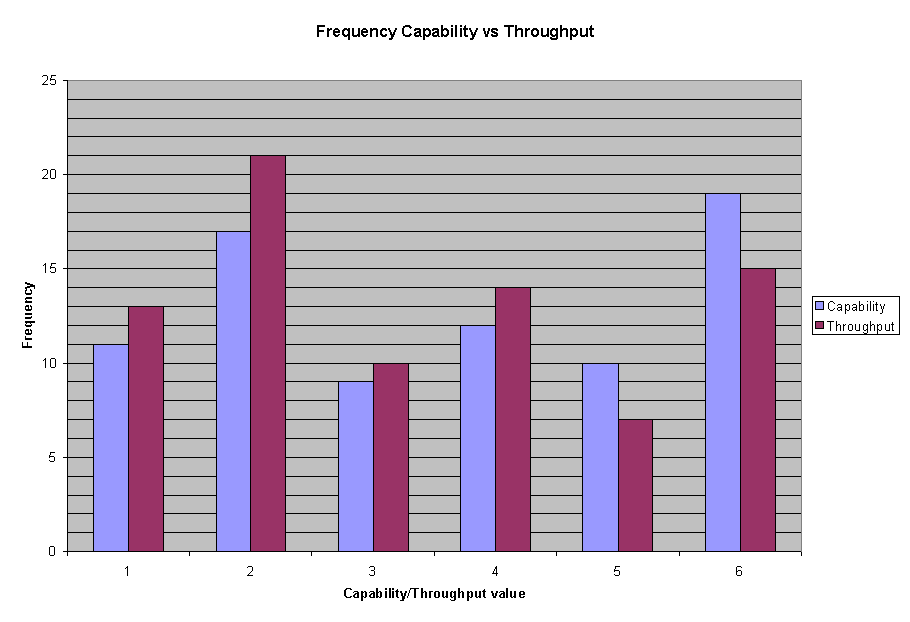The following chart compares the frequency of occurrence for values of capability and throughput. The values throughput exceeds capability tend toward the low to middle portion of the scale. This is another view of throughput being less than the capability of the system.
Conclusion
Variability in the output of a member of a system limits the capability of the system. When preceding steps do not supply the necessary products, the remaining steps in the system cannot perform to the maximum capability. Another feature of the variability is creation of work in process. Work in progress, inventory, is scattered through the system, it is not located to protect a constraint. In some places, there is no inventory, in others there is a large amount.
This was an interesting exercise. I was surprised that the outcome was as good as it was. I had expected more steps to be limited by lack of product.