
Mostly chapter 4; some of 5
Newton’s Laws of Motion MADE SIMPLE
Your entered in the 100 m dash finals in the Olympics; you’re in the starting blocks; your set.... and you start thinking about Physics class, wondering what are the principles of physics that will allow you to get the fastest start?
Principles: You are using Newton’s 2nd and 3rd Laws of Motion.
Straightening legs pushes on upper body and accelerates it up and down the track. Requires that you push as hard as you can against the blocks (first the back leg, then the front leg) -- The reaction of these forces on your feet are what accelerates your entire body forward. Timing critical -- + must start with or after the gun!

FORCE -- a vector quantity that represents a push or pull on an object.
Forces are not directly observable -- we observe their effect -- the change produced by a force.
YOU live in a world where two types of forces dominate: gravity, electromagnetic.
Deep down in the atom in the nucleus the so-called strong and weak forces dominate in how nucleons (neutrons, protons) interact, how quarks and other elementary particles combine and interact to determine radioactive decay, how nuclear fusion works, what happens in star interiors, etc.
Everyday Forces
Objects fall because of the force of gravity;
Automobiles move because the tires push against the road through FRICTION;
He Balloons rise and boats float because of buoyant forces;
Your TV or computer monitor can produce images because electrons can be pushed and pulled by other electrons or by magnetic fields;
Chemical reactions occur because of attractive and repulsive electromagnetic forces {includes metabolism, photosynthesis, bone growth} [chemical bonds are electrostatic -- remember + and - charges attract].
Galileo Deduced -- Under ideal frictionless conditions, a body left to itself would continue to move forever with uniform velocity.
First Law (N1) : A body at rest remains at rest, and a body in motion continues to move at constant velocity unless acted upon by an external force.
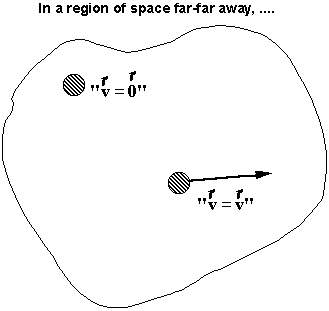
Tendency of a body to continue in its initial state of motion (either at rest or uniform velocity called
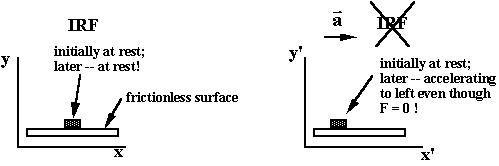
inertia.A reference frame in which First Law is obeyed is called an inertial reference frame (IRF). Any other reference frame moving at constant velocity with respect to an IRF is also an IRF.
Any frame of reference that accelerates relative to an IRF IS NOT AN IRF.
Although the earth is rotating on its axis and going around the sun which is orbiting around in the Milky Way galaxy, which is headed for the Restaurant at the End of the Universe -- the surface of the earth is ~ an IRF.
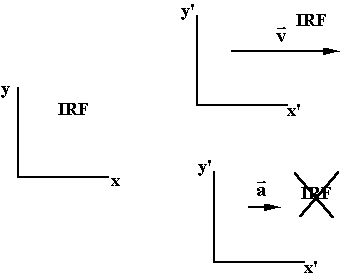
Is a merry-go-round an IRF?
noMass and Newton’s Second Law
2nd Law: An external force acting on a body gives an acceleration in the direction of the force and has a magnitude directly proportional to the magnitude of the force and inversely proportional to the mass of the body,
N2 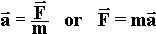
![]()
VALID ONLY IN AN IRF.
N2 used to define mass: If two bodies of different masses are subjected to identical forces, the accelerations will be inversely proportional to the masses:
![]()
For the same force, big masses accelerate small amount; small masses accelerate large amount; large masses have lots of inertia}.
Use a Rubber Band to apply a "standard force" (
DL constant):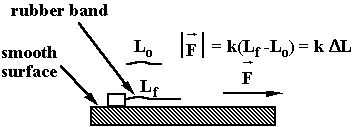
Through ![]() we can relate
all masses to the standard Kg.
we can relate
all masses to the standard Kg.
Units of Force: a standard force can be generated by accelerating
a standard mass by a "standard acceleration"{ 1 m/s
2 } Using N2:1 Newton is force required to accelerate the standard kg at 1 m/s
2.(Note goes back to standards of distance(m) and time(s).
[N] = kgm/s
2(Unit of force in British System is the Pound Force: 1 lb = 4.448 N).
A world record holding jet engine car has a mass of 4000 kg and its engine can develop a thrust of 80,000 N. Assuming no friction, what acceleration could the car achieve?
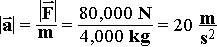
(Very high acceleration -- equivalent to ~ 2 g’s.)
In practice how do we measure mass? Using a balance:

Electronic Balance: Use a transducer that is sensitive to compression or tension, giving an electrical signal proportional to WEIGHT. Must be calibrated (and be very stable!!). [Quartz -- produces a voltage when squeezed proportional to force; some metal alloys increase electrical resistance when stretched].
Forces are often calibrated by matching with a known weight.
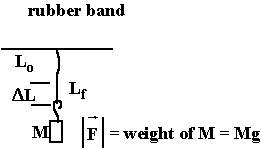
Spring balance; again calibrated with known "weights" (masses).
When two or more forces are applied to an object:
Find resultant force: 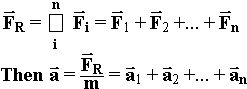
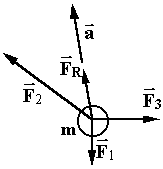
 [This is N1 - Newton’s First Law!!!!]
[This is N1 - Newton’s First Law!!!!]
Things only accelerate when a non-zero net force is being applied. When you throw or kick a ball, during the time you are in contact with the ball -- what are the forces on the ball? Qualitatively, what is the acceleration? After the ball is free of your hand or foot, what are the forces? acceleration?
Newton’s Third Law
Take your little finger and push down on the table has hard as you can (no pain, no gain!) -- Should feel table pushing back. Object A cannot exert a force on Object B without Object B exerting a force on A (equal in magnitude and opposite in direction):
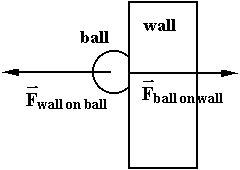
Newton’s Third Law (N3): Whenever a body exerts a force on another body, the latter exerts a force of equal magnitude and opposite direction on the former.
These coupled forces are called a action-reaction pair. Which is action which is reaction? doesn’t matter!
TO PREVENT "MISTEAKS": Note -- the two oppositely directed forces are acting on DIFFERENT OBJECTS. Therefore they never cancell each other out!!!!
This includes objects that interact through "FIELDS":
Gravitational, Electrical, Magnetic fields
Gravity "happens" because objects have mass.
Electrical forces -- because they have charge.
Magnetic forces arise from moving charge (e.g., electrical currents);
[sometimes atomic level currents!!]
Every object in the universe pulls on every other object in the universe -- and all the other objects pull back!! All forces come in pairs.
When the Shuttle Encounters Mir in Space:
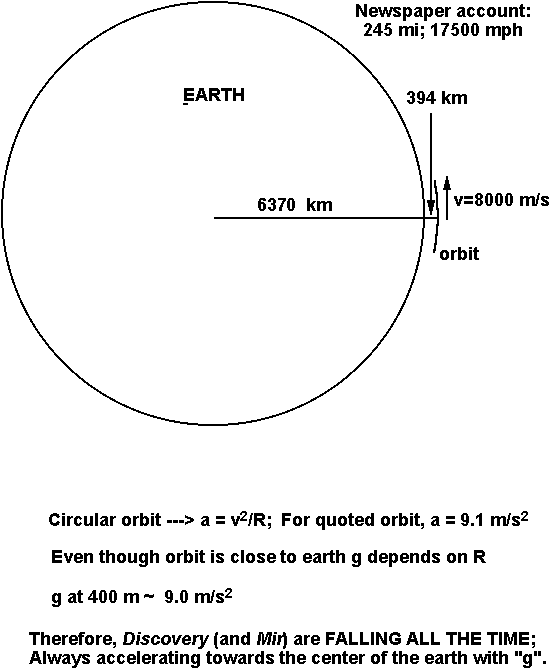
Question:
Is a coordinate system that is accelerating in a straight line an IRF? -- Describe the motion of a projectile viewed from an accelerating coordinate system:
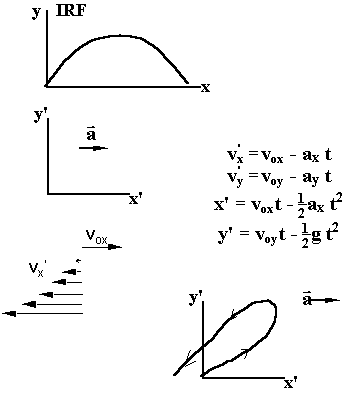
objects at rest in gravitational field
Book on Table:
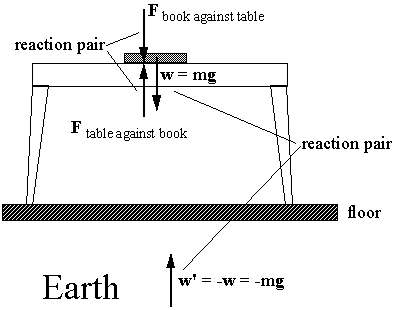
Book is at rest -- F
total = 0; Ftable against book = - wIF table not there, w would remain; i.e., F
total = wTherefore book accelerates towards earth. ( w’ becomes unbalanced also; thus, earth accelerates towards book).
Setting Up N2,N3 Problems
Secret is isolating the object and the forces on it. Consider a block of mass m on a frictionless horizontal surface being pulled with a string by a force F.
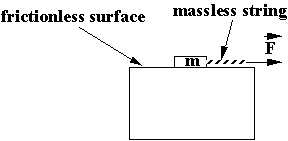
Forces on block:
1. weight of the block, w.
2. Contact force F
3. The contact force T exerted by the string on the block.
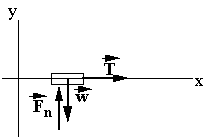
This drawing is called a free-body diagram; isolates the body and shows the forces exerted on it.
F
n and w have equal and opposite directions -- no acceleration in vertical direction.The only net force is T; therefore, T = ma
x"String Theory"
Apply N2 to the string:
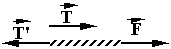
![]() is the force on the string exerted by the
block.
is the force on the string exerted by the
block. ![]() = -
= -![]() .
. ![]() is in the same
direction as
is in the same
direction as ![]() .
.
If string is taut, its acceleration = acceleration of the block, ax.
Let ms be the mass of the string: F - T’ = msax
IF m
s ~ 0 , then we see thatIf we look at a segment of string of mass
Dms :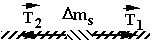
![]() is the force exerted on this segment by the
part of the string to the right.
is the force exerted on this segment by the
part of the string to the right.
![]() is the force exerted on this segment by the
part of the string to the left.
is the force exerted on this segment by the
part of the string to the left.
Because Dms ~ 0, we know that T1 = T2 = T -- called the TENSION in the string. Each segment exerts a force T on its neighbors. A "massless" string therefore has a constant T throughout length and transmits F to the contact point undiminished.
HOLDS for massless pulley or a frictionless peg as long as there are no tangential forces on string between two points considered.
STRINGS CANNOT PUSH.
Sliding without Friction
Consider a block of mass m that slides down a fixed, frictionless surface inclined at an angle
q to the horizontal. {Common Sense -- block slides along incline!!}
Resolve ![]() in x and y
directions (project
in x and y
directions (project ![]() along x and y axes).
Note
along x and y axes).
Note ![]() is in y direction.
is in y direction.
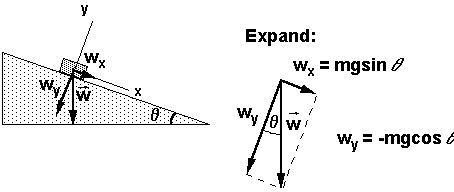
{When the sides of angle 1 are perpendicular to the sides of angle 2, angle 1 = angle 2}.
Net force in y direction: F
n - mg cosqWe set this = 0 because a
y = 0, i.e., block accelerates along incline.I.e., N2 says:
SFy = Fn - mg cosq = 0; therefore Fn = mgcosqx components:
SFy = Fn - mg sinq = max
therefore ax = gsin
qFor constant
q, ax is a constant, including being independent of mass, m. Therefore, all of the [a = constant] equations apply. Galileo worked on this as one of his experimental systems. Deduced many of the kinematic equations.CHECKS: a
x ~ sinq:Lower the incline towards
q = 0; ax ---> 0 (horizontal -- book on table)F
n ---> mgRaise the incline towards
q = 90; ax ---> g (vertical -- free fall)F
n ---> 0
Elevator Problem
A person stands on a scale fastened to the floor of an elevator. What does the scale read when elevator accelerates up? down? at constant v?
Since person is at rest in elevator, a
Forces on person are ![]() upward (exerted by
scale)
upward (exerted by
scale)
and weight, ![]() downward (exerted by
gravity).
downward (exerted by
gravity).
The net force is F
n - w upward in direction of acceleration,N2 gives: F
n - w = ma or Fn = w + ma = mg + ma.The force ![]() exerted by the person on the
scale determines the scale reading; BUT
exerted by the person on the
scale determines the scale reading; BUT ![]() and
and ![]() are a action-reaction pair; EQUAL IN
MAGNITUDE.
are a action-reaction pair; EQUAL IN
MAGNITUDE.
When elevator accelerates upward, apparent weight = true weight + ma.
Downward acceleration, ![]() : Net force on
person must be downward; i.e., mg is > F
: Net force on
person must be downward; i.e., mg is > F
Choose Down +, w-F
n = ma’or F
n = w -ma’ = mg - ma’Scale reads F
n in magnitude; Therefore,When elevator accelerates downward, apparent weight = true weight - ma
’.What if a’ = g? What if a’ > g?
What if a = 0?
"
GOLD BRICKS"A woman needs to carry three bricks of gold across a bridge. The bridge will collapse under weight greater than that of the woman plus one gold brick. How does the woman get the bricks across the bridge?
Proposed Solution: The woman juggles the gold bricks. Just keep bricks in air!

WRONG!
As the woman throws a brick UP she must apply a force, and because of N3 an equal (in magnitude) force is applied on her DOWNWARDS, so that during a short period of time the force (DOWN) on the bridge will be more than the weight of the woman plus one brick -
collapse...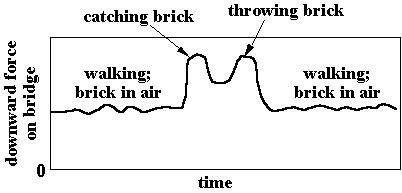
FRICTION
Whenever two objects are in contact, and we try to slide one on another, there is a force which opposes that motion = FRICTION.
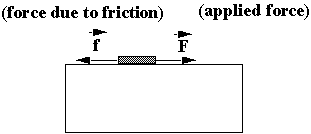
If you adjust ![]() so that
so that ![]() = constant, then
= constant, then ![]() .
.
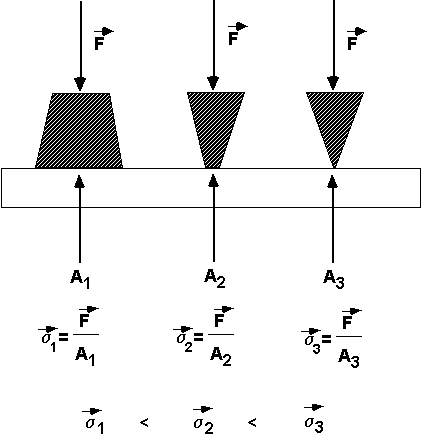
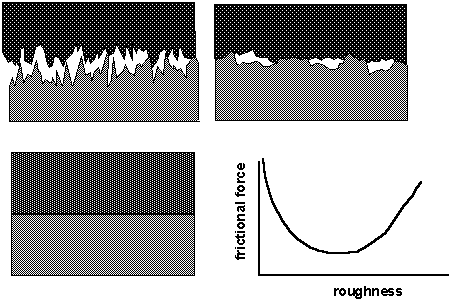
Common origin of friction is surface roughness:
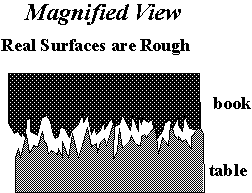
Asperities (bumps and points) interact and push on each other with enormous STRESS (Stress = Force/area ---like pressure except highly localized). Stress is what causes deformation and fracture of materials. Holding a knife by its handle (large A, small stress on your hand) vs. holding it by its point (small A, large stress). First case -- no pain. Second case -- PAIN. PAIN is due to deformation and tearing of tissue.
High stress lifts the mass (which eats up energy) -- in principle, should get this energy back, but you don’t get it all back, due to impact.
High stress causes asperities to deform plastically (irreversibly -- like clay; eats up energy.
High stress causes asperities to fracture off (you often see little wear particles); again eats up energy.
These energy-eating processes result in this frictional force -- totally wasted - (most of the energy ends up as heat).
Removal of material called WEAR. (look at your shoes; steps of an old building, "Neptune’s Toe".
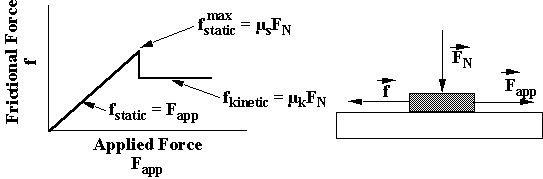
Static Friction. You start pulling on an object at rest, increasing the force from F
1 to F3, where it just starts to move.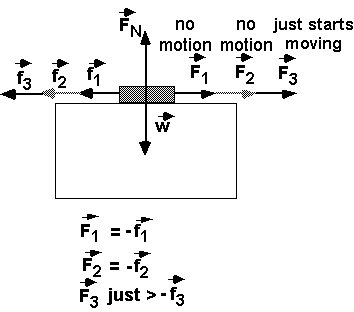
f
3 is defined as the static force of friction. Found empirically (experimentally) that fstatic = mstatic FN , where FN is the normal force (holds the two surfaces in contact), in this case = |w| in magnitude.If table is tilted, F
N is still the normal force < w.m
s is called the coefficient of static friction; depends on the objects in contact. Ranges from 0.1 (lubricated surfaces) to ~ 1.00). Varies quite a bit (depends on surface conditions).Better to write that the opposing static force of friction is:
![]()
Equality only at the instant the body is about to go into motion;
Before that instant, f
static = - Fapplied (assuming Fapplied || surfaces)Kinetic (sliding) Friction. Once object is sliding, find that
![]()
Takes less force to keep it sliding than to get it sliding (heavy box on a kitchen floor).
Define another coefficient, µ
k (Coeff. of Kinetic Friction),![]() ;
;
direction of f
kinetic opposite direction of motion.{Note these are empirical laws -- only approximate}
For flat surface: F
N = w; not dependent on areaApproximate Coefficients of Static and Kinetic Friction
Graphical Representation
Friction strongly depends on adhesion (the sticking of two materials together; e.g., rubber on glass-strong adhesion).
Breaking adhesive bonds eats up energy -- requires force.
Take two metal objects with relatively flat surfaces:
Atomically clean surfaces can be welded together in vacuum by contact.
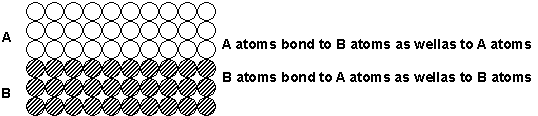
Penny on the Railroad Track.
Lubrication
Liquids and gases flow over themselves easily (low viscosity). When put between two surfaces, form an ordered layer of "slippery stuff". Keep asperities from touching; prevent local welding; lower friction significantly!! (OIL in your car -- don’t forget to add oil!).
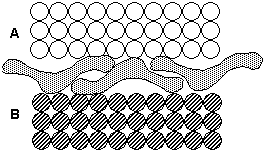
Ice skater -- weight of skater increases pressure under blade -- causes ice to melt - forms a lubricating water sheet; bobsled, luge.
f normally does not depend on area. Take a block of mass m, weight mg. Measure sliding friction on edge, and on side; ~ same.
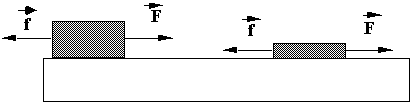
"Model" -- ![]() depend on
microscopic contact area:
depend on
microscopic contact area:
f ~ A
microscopicBut
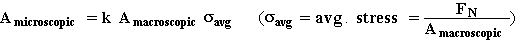
Therefore, f ~ k F
N, independent of Amacroscopic.Rolling Friction. Balls and Wheels normally offer less friction than sliding (ball bearings, tires). Rolling Friction is the friction you have to overcome just to keep round objects moving. It is due to dissipation of energy from making and breaking contact between object and surface. µ
rolling typically 0.001 - 0.1 (steel wheels on rails: ~ 0.001 very low).This is not the friction that pushes the automobile.
IF tire did not deform, contacts surface at a line. While rolling along at velocity v, the points on wheel have a SPEED = v:
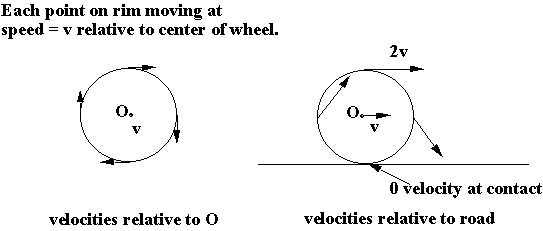
In car, wheels rolling without slipping implies that tire surface in contact with road is at rest relative to the road. (think this way: rim is moving backward with v, axle moving forward with v; cancel).
A rolling wheel experiences only rolling friction. However, if you apply torque ("Rotational Force") to speed up or slow down, the tire interacts with road through the STATIC FRICTIONAL FORCE.
So when you accelerate, engine transmits forces to axle, turning the tire, which pushes against the road through static friction.
µ
s (tire dry road) typically 0.7 - 1.0 ; µk typically 0.3-0.7.IF too much torque applied, wheels spin relative to road, using µ
k. When stuck, try to reduce torque (manual transmission -- try 2nd, 3rd gear) so that you use µs.Braking: brakes slow down rotation of tire -- STATIC FRICTION wants to keep v
contact = 0; as long as f < fmax, wheel does not slip.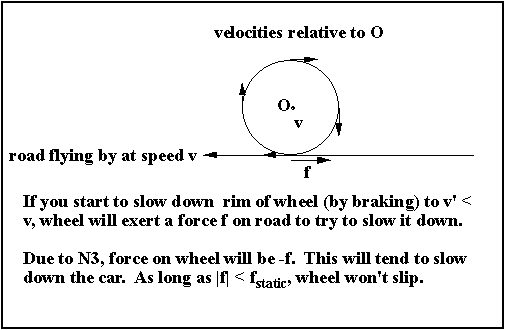
IF you lock the wheels, tire/road, instead of static friction, you have Kinetic Friction which is smaller -- (melted rubber lubricates; ice, gravel). YOU SHOULD PUMP BRAKES!! to keep wheels rolling (unlocked) during slowing down. {trying for a
max so distance to v= 0 is minimized :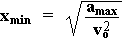 }
}
Car in icy skid: You put on brakes and back of car starts moving toward front (spin) -- often a result of locked back wheels and rolling front wheels; once car starts spinning, f
front > fback so front acts as a pivot, back swings around. If you have an open road (don’t need to stop) turn front wheels so they will roll with the spin this reduces greatly ffront; by pumping brakes you try to regain µstatic in the back (back wheels rolling). so now you ffront < fback; torque should be reversed (opposed to spin). Sometimes, gently pushing on accelerator generates additional torque opposing the spin. Roll of Anti-Locking Brakes -- to minimize time sliding -- keeps wheels rolling but braked.Truck with Locked Back Wheels on Incline
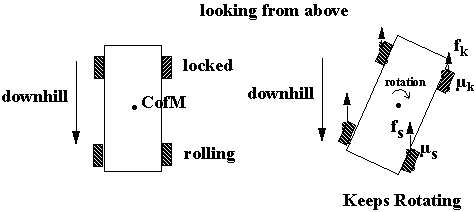
To stop rotation, unlock the back wheels (pump) to gain back µ
s and turn front wheels to maximize rolling of front (i.e., downhill).
Racing Slicks: BIG, WIDE, and TREADLESS -- For Drag Racing -- they pour sticky gooy stuff under the tire: SPIN LIKE CRAZY.
What’s going on? -- Found that by sacrificing tire -- can get more acceleration at very high tire speeds using µ
k rather than µs.Wide tire -- force of friction same as narrow tire -- no advantage. Reason for big, wide tire: COOLER. Reduces Melting of Tire which would provide lubrication. Sticky Goo -- to reduce lubrication, raise µ
k. Greater traction also results in reduced time in the slip part of race -- eventually µs kicks in -- then acceleration limited by power of engine.
The Tablecloth-Table Setting Trick
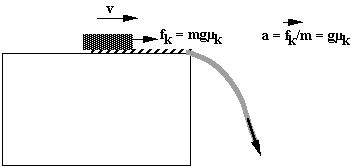
During the downward pull on the tablecloth, the force applied to the tablecloth increases rapidly in time. There are three phases to the motion of a dish during the pull.
a. In phase 1, the dish is in contact with the cloth, stationary with respect to the cloth, and accelerates with the cloth. Sketch the dish and the cloth at a time during this phase of the motion.
Show ALL the force vectors acting ON the dish. Draw velocity vectors and acceleration vectors (if they exist) for the dish. (For simplicity, here and below show the dish as a box.)

We shall assume that this time interval is so short, NO velocity is acquired; no distance is moved.
b. In phase 2 of the motion, the dish is in contact with the cloth and moves with respect tothe cloth as the cloth slips out from under it. Sketch the dish and the cloth at a time during this phase of the motion. Show ALL the force vectors acting ON the dish. Draw velocity vectors and acceleration vectors (if they exist) for the dish.
c. In phase 3 of the motion, the dish is in contact with the table and slides to rest. Sketch the dish and the cloth at a time during this phase of the motion. Show ALL the force vectors acting ON the dish. Draw velocity vectors and acceleration vectors (if they exist) for the dish.
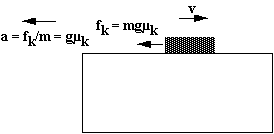
(Do this as out-of-lab problem OLP #5.) Derive the expression below for d, the distance moved by the plate.
d = (1/2) mkc g t2 [ 1 + (mkc/ mkt)] (1)
In Eq. (1), g is the acceleration due to gravity; t is the time required to pull the cloth out from under the plate (i.e., the time duration of the "phase-1 motion" (see above); and mkc and mkt are the coefficients of kinetic friction for, respectively, the plate on the cloth and the plate on the table. [HINT: Use Newton's second law, Fnet = ma, to obtain accelerations in terms of m and g for the phases 2 and 3 of the motion diagrammed above. (Assume that the distance moved during phase 1 is negligible.)
a2 = g µkc ; s2 = 1/2(gµkc) t2 ; s3 = vo2/2a3 stotal = s2 + s3; a3 = g µkt;
vo2 = 2 a2s2 = 2 a2 (1/2(gµkc) t2 ) But it together and get (1).
2. (OLP #6) Is Eq. (1) physically reasonable? {Y, N, U, NOT} [ HINT: Consider dimensions and the predicted magnitude of d for both realistic and extreme limiting conditions.]
3. (OLP #7) Explain why, physically, the displacement d of the plate is independent of the mass m of the plate and the area A of contact of the plate on the cloth or the table.
4. (OLP #8) Plug the measured values of d, and coefficients of friction roughly measured by the staff (mkc = 0.1, mkt = 0.2) into Eq. (1) so as to yield t. Do you think this t is physically reasonable?{Y, N, U, NOT} Can you think of ways to measure t directly? {Y, N, U, NOT}
5. (OLP #9) So far, in our work on mechanics, we have assumed that extended objects can be treated as point particles. Thus, in the derivation of Eq. (1) we ignored "torques" which might act to rotate the objects on the tablecloth. Explain why it's a good idea to avoid placing tall high-center-of-mass objects such as the flower-vase-plus-flowers of Fig. 1 on the slip-out-trick tablecloth.