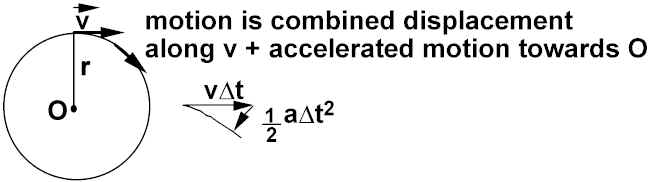
Chapter 5 Circular Motion; Gravity
Any object moving in a circle is always changing direction of motion. Therefore is accelerating.
For circular motion with constant speed v, GEOMETRY and Kinematic equations require this acceleration towards O to be:
![]() , a points
towards O.
, a points
towards O.
Centripetal = "center seeking"
If T is the period of the motion = time for one revolution,
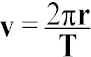
By N2, to accelerate requires an unbalanced force:
![]() , where F points towards O.
, where F points towards O.
What produces the force? strings, rubber bands, gravity (sun, earth, moon, black holes), electric charge (proton attracts an electron = Hydrogen atom), FRICTION. Is there an action - reaction pair here? YES.
WHAT HAPPENS WHEN YOU SUDDENLY REMOVE F?
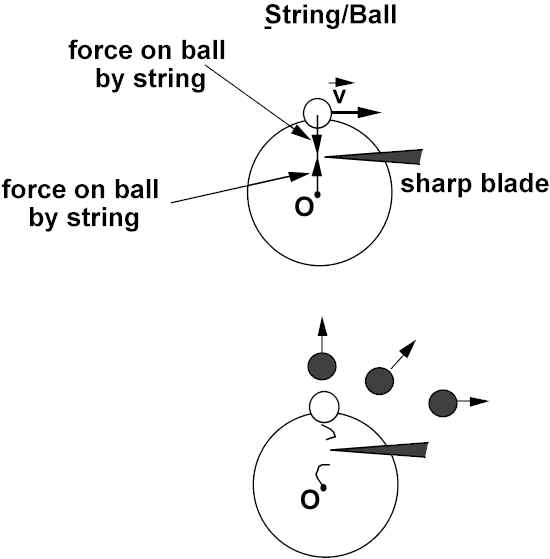
If moving on a frictionless, horizontal surface, when string breaks, ar goes to 0. At that point, v= vox. There are no forces on ball, therefore moves away with constant velocity vox.
(If rotating in a vertical plane, launches a projectile with vox.
If you swing a ball in a horizontal circle about your head, can the string be exactly horizontal?
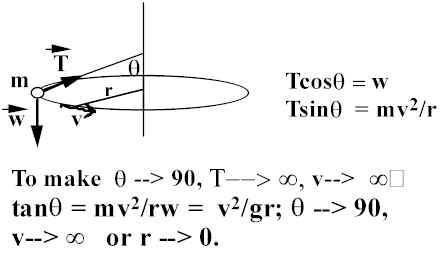
Frictional Centripetal Force
A car approaches a level, circular curve with R = 45.0 m. If the concrete is dry, what is the maximum speed the car can negotiate the curve at constant speed? (Take µs = 1.2).
Given: r = 45 m; FIND: v (max. speed).
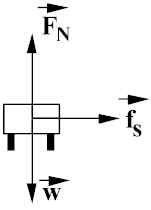
To go around the curve, must be ar
different from 0, therefore a Fr different
from 0. Provided by static friction between tires and road. Maximum frictional force: ![]() .
.
The centripetal force required to keep car going in circle is mv2/r.
When you speed the car up faster than vmax, where
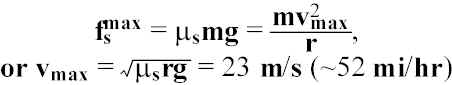
Note: independent of m (m’s cancel out).
Graph:
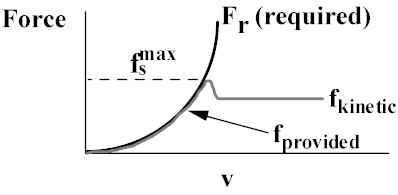
If road conditions, tire conditions lower µs, this can greatly reduce vmax. Flat road -- Bad News!!
Skaters race on a flat track: How do they get around the turns?
(Its a frictional force!!)
Banking the Curve -- gives a component of normal force towards the center of the circle; Find q so that no frictional force is required to have car negotiate curve.
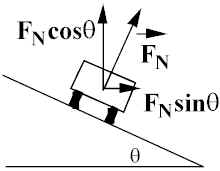
Horizontal Direction: ![]() ;
;
Vertical Direction: 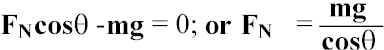
Substitute for FN : 
Take v = 100 mph (44.2 m/s), r = 100 m; q ˜ 63° (very steep).
Four aluminum cubes of identical mass and surface polish are put on a turntable as shown:
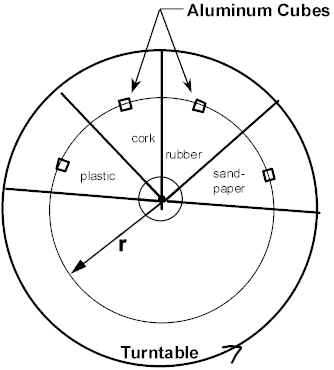
Each cube is on a different surface (smooth plastic, cork, rubber, sandpaper). As the speed of rotation of the turntable is gradually increased, describe what happens and why.
A 0.5 kg toy car travels down a plastic track at an angle. At the bottom there is a loop-the-loop, 0.409 m in radius, r. What is the minimum speed (in m/s) that the car must have at the top of the loop to stay on the track?
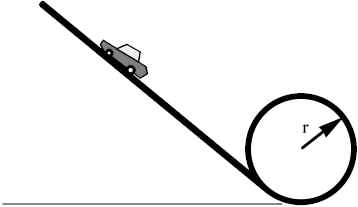
A. 8.18 B. 2.86 C. .64 D. 2.0 E. 4.0
Newton’s Law of Universal Gravitation
Between every two masses in the universe there is a force of attraction between them that is directly proportional to the product of their masses and inversely proportional to the distance between them.
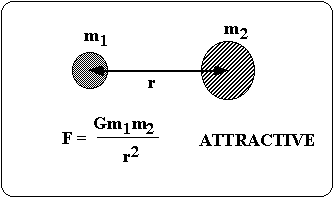
G is the universal gravitational constant, given by
G = 6.67 x 10
-11 Nm2/kg2 (BIG G)(assumed that radii of objects << r; treated as point masses).
Put two 1 kg masses 1 meter apart on a table. Do they slam towards each other? what is the force?
F = Gm
1m2/r2 = (6.67 x 10-11 Nm2/kg2) (1kg)(1kg)/(1m)2 F = 6.67 x 10-11 N (very small!!)If m
s ~0.5, what is the maximum static friction force that table could provide? fmax ~ 0.5 mg = 0.5 x 1kg x 9.8 m/s2 = 4.9 N! (11 orders of magnitude < than Fgrav.Measurement of G
in Laboratory determines the mass of the earth!! Performed by Cavendish (English) in 1798.
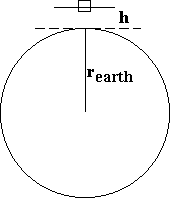
r = r
earth + h ~ rearth = 6.371 x 106 m; Therefore, on 1 kg mass, F = G (1kg) mearth/rearth2 . But at surface of earth, from F= ma, F = (1kg)g, where g is the measured acceleration due to gravity.Therefore, m
earth = rearth2 g(1kg)/G = 5.98 x 1024 kg !!!Knowing the mass of the earth, we can now get the acceleration of gravity as a function of distance from the center of the earth:
g = G
mearth/r2. (if you plug in rearth you get ~9.81 m/s2)So, What is the difference between LITTLE g and BIG G?
Note: g changes with altitude; also latitude--earth is an oblate spheroid: bulges at equator; correction for centripetal acceleration; nonhomogeneity of mass.
On the MOON
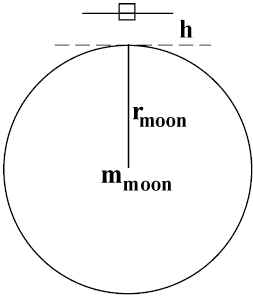
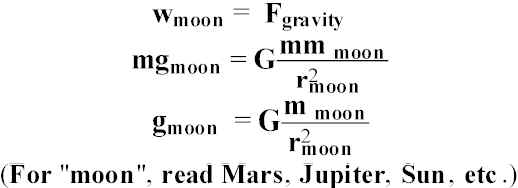
For moon, r
moon = 1.738 x 106 m; mmoon = 7.34 x 1022 kg,g
moon = 1.62 m/s2 (~1/6 gearth) If you weigh 150 lb on the earth, you will weigh 25 lb on the moon. gJupiter = 2.37 gearth; you would weigh 355 lb.Satellite Motion
(Newton actually considered the issue of launching objects into orbits). Assume circular orbit:
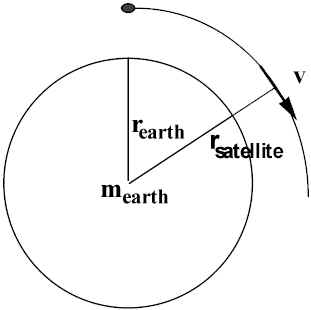

This equation relates r
satellite to vorbit. ONLY ONE FORCE ACTS ON satellite -- Gravity.Geosyncronous Satellite -- stays fixed above a point on earth’s equator as earth rotates. Find r. v = s/t = 2
pr/T ( T = period = 24 hr x 3600 s/hr).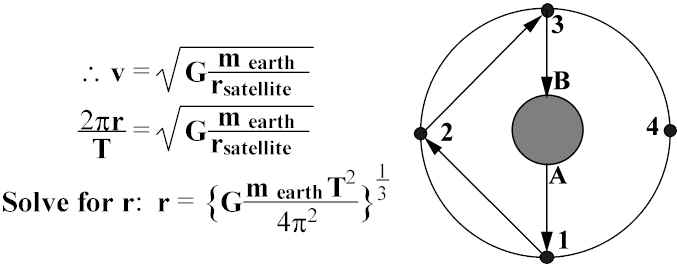 rgeosync = 4.22 x 107 m ~26,200
miles
rgeosync = 4.22 x 107 m ~26,200
miles
AN ASIDE: Which countries still use the British System?
Tonga, Southern Yehmen,.and USA!!!!
Southern Yehmen is in civil war and may not exist.
------
What is the gravitational force between an electron and a proton in the hydrogen atom? Take: r = 5.3 x 10
-11 m.m
e = 9.11 x 10-31 kg; mp = 1.67 x 10-27 kgF
grav = Gm1m2/r2 = (6.67 x 10-11 Nm2/kg2) (9.11 x 10-31 kg) x(
1.67 x 10-27 kg)/(5.3 x 10-11 m)2F
grav = 6.6 x 10-44 NF
electrostatic = 8.2 x 10-9 N (over 1036 times stronger).Weightlessness
Already looked at falling elevator w = m(g-a) = m(g-g) = 0.
Same for orbiting shuttle as in falling elevator; always accelerating towards earth to as if falling!!! Therefore, you fall at the same rate as shuttle, objects float relative to shuttle, can’t tell which way is up.
Plane in parabolic arc simulates orbiting: get a few seconds of nearly free fall.
If you went far, far away from planets and sun, F
grav decreases with 1/r2, then "weightless".