be an
unbalanced force applied to an object, and let 
be a resulting displacement. If FSimple Concepts Involving Work and Energy
Let be an
unbalanced force applied to an object, and let be a resulting displacement. If F
along 
, then the WORK done by , W, is given by W = F|| x d = dot product of the two vectors and .
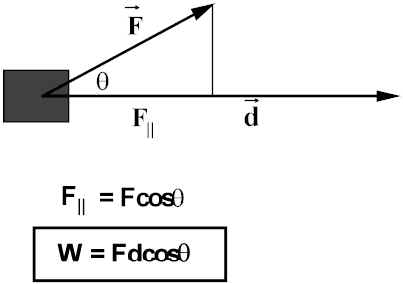
When
q = 0, F is parallel to d, cosq = 1, W = Fd.Units of W = Newton-meters (N-m) 1 N m = 1 Joule.
When
q = 90°: F is perpendicular to d, cosq = 0, W = 0! Carrying a weight corresponds to W = 0.IF d = 0: Pushing against an immovable object, W = 0.
Both cases body uses chemical energy for muscles to exert these forces (you get tired, need more Twinkies to keep going)--in terms of mechanical work performed: ZIP!
Work down lifting a box
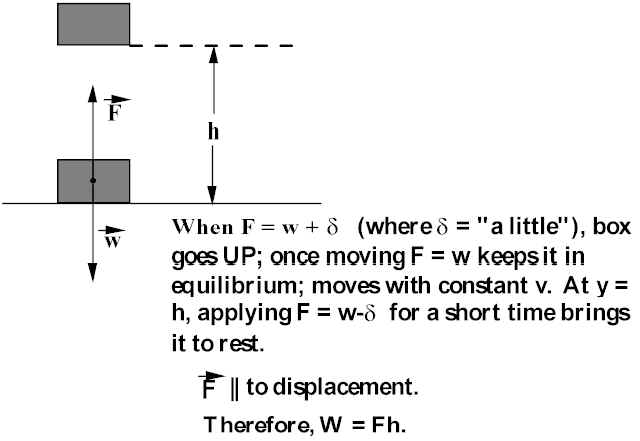
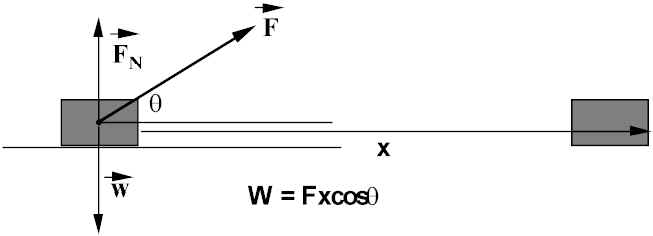
Force not in same direction as displacement:
Work keeping a satellite in circular orbit above earth:
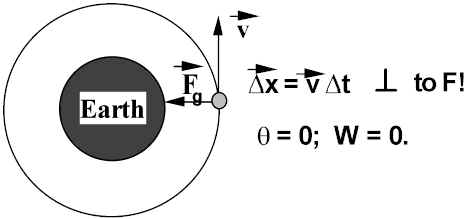
NO work done by gravity to keep it up. (What about Launch!!!!)
Work done in stopping a car:
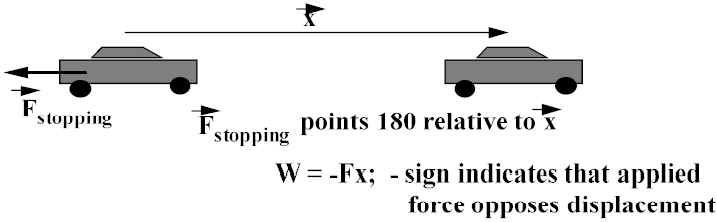
Mechanical Energy: traditional definition = the ability to do work.
Moving objects can do work (bowling ball displaces pins; hammer pushes in nail; car creams cow) energy of motion = kinetic energy.
Suppose a "bullet" of mass m moving at v
o mushes into a block of soft clay and experiences a constant force F (decelerating at a constant rate, a).
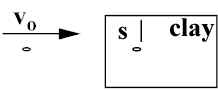
The force required to slow down the bullet is F = ma, where a is the deceleration. The work done through the distance s, W = Fs = mas.
During the deceleration, v
2 = vo2 + 2as; or as = 1/2(v2 - vo2)or Work done ON OBJECT = 
. (would get same result for non-constant F and a).
The mechanical work done on the object = the change in kinetic energy; 
.
If W is positive, KE increases; IF W is negative, KE decreases. 
-- often called Work-Energy Theorem
(Net work done = change in kinetic energy
Suppose a car of mass 1200 kg falls vertically a distance of 24 m (starting from rest; i.e., v
oy = 0).(a) What is the work done by gravity on the car?
F
grav = mg; Dy = 24 m; Force and displacement in same direction (down).
F
grav = Fnet because gravity is only force acting on car.(b) Find final velocity of car.
Using constant acceleration (g): 
.
Using Work-Energy Theorem:
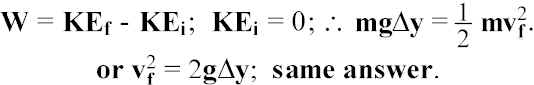
Plug in: v = 22 m/s.
Variable Force
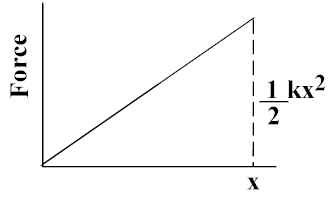
Suppose F acting on a mass m depends on x; e.g., F = kx We divide x into little increments,
Dxi, where Fi is the average force over that interval:
Total work going from x
1 to x2 = Wtotal = S FiDxi = area under curve!! (C word = integral of F from x1 to x2) and DKE = Wtotal.For linear force, F= kx, Area under curve from 0 to x
f =
.
A mass m is moving in a straight line at velocity v
o. It comes into contact with a spring with force constant k. How far will the spring compress in bringing the mass to rest?A spring exerts F proportional to x in both compression and extension (for reasonable x).
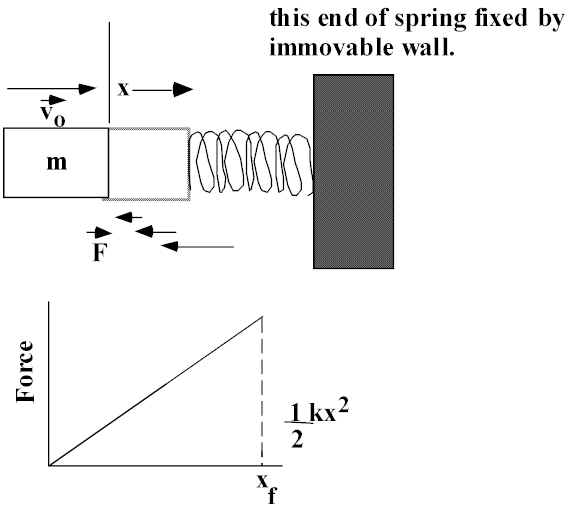
Change in KE = KE
f - KEi = 0 -
mvo^2. Work done by F on mass, W = -
kxf^2. Therefore, kxf^2 = mvo^2 or 
.
IF we use object and compress spring this same distance (x
f = xo) and let go, what is final KE and v? Work done by F on mass, W = +
kxo^2.
Change in KE = KE
f - KEi =
mvf^2 + 0. Therefore, mvf^2 = kxo^2. Since
xf = xo, we see that: |
| = |
|. Since we take a 
, ± does not give direction. Have to go to PICTURE; conclude that 
.
Potential Energy
Object in motion -- has kinetic energy. With or without motion, objects can have Potential Energy -- "potential to do work".
Examples: Object (Mass) at top of a building
Mass pushed up against Compressed Spring
Water behind a dam
A drawn bow
For mechanical systems -- best to think of this type of energy as "energy of position".
For spring, we do work compressing the spring -- once compressed, spring ready to deliver the energy back by accelerating a mass and giving it KE.
When you compress the spring a distance x, the work done to compress the spring =
; the
work the spring can now deliver W = (Conservative Force) The spring is said to contain
potential energy U = W = . When you release the spring, you can deliver this
amount of energy to a mass m, so: mv
.
Gravity is a conservative force, also. Work done in lifting mass m a distance h = W = mgh. Therefore, for h > 0, U = W = mgh.
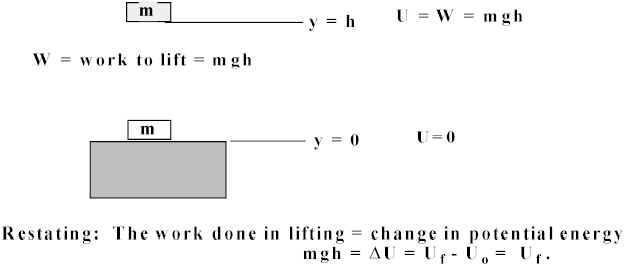
So Gravitational Potential Energy (in vicinity of Earth’s Surface) is
U
Suppose you throw a ball straight up with velocity v
o. from yo = 0; set Uo = 0. Know that:
.
REMEMBER: holds for going up and going down!!!!
MULTIPLY BY 
:
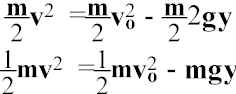
Rearrange: 
(1)
The change in the potential energy = change in KE. Gives |v| for any allowed y. (Max y
occurs when v = 0: 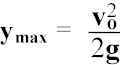, as previously calculated).
Another form of Eq. (1): U
final - Uinitial = KEinitial - KEfinal; we can collect "initial" and "final" so that:
U
SUM = Total Mechanical Energy = E
HOLDS FOR ALL CONSERVATIVE FORCES. "initial" is whenever you start the problem, "final" is whenever you want an answer. NOTE that if y
final = yinitial, i.e., come back to where you started, E the same, independent of path.Nonconservative forces - E depends on path. Best example is frictional forces. You do work against them, but you can’t get it back (goes into heat).
Conservative: U
initial + KEinitial = Ufinal + KEfinalNon-Conservative: U
initial + KEinitial = Ufinal + KEfinal + Q(heat)Q represents lost mechanical energy; if we include, Energy still conserved.
Suppose you throw three balls of equal mass m off a cliff with the same speed, v
o, but at three angles relative to the horizontal shown in figure: 0°, ±45°. Which ball, 1, 2, or 3 strikes the ground (distance h below) with the greatest speed? Neglect air resistance.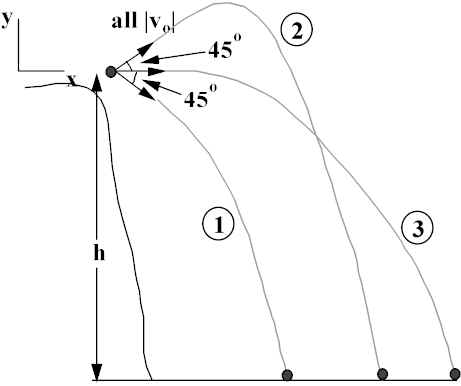 
Answer: They all hit the ground with the same speed. In all three cases, at throw, 
. At collision
with ground,
.
Therefore,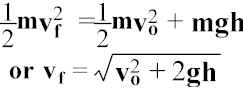 
independent of m!!
Could be all different mass; same result.
Skier with Friction
A skier of mass 80 kg starts from rest down a slope where
Dy = 110 m. The speed of the skier at the bottom of the slope is 20 m/s.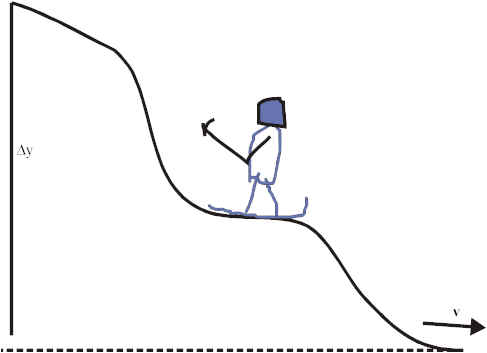 
(a) Show that the system is nonconservative.
Given m, v
o, vf, and h. Find Ei and Ef to test for conservation.E
i = KEi + Ui = 0 + mgDy = (80 kg)(9.81 m/s2)(110 m) = 8.6 x 104 JE
f = KEf + Uf = (1/2)mvf2 + 0 = (1/2)(80 kg)(20 m/s)2 = 1.6 x 104 JSince E
f < Ei, system lost energy -- non-conservative.(b) How much work is done by the non-conservative force?
Q = E
i - Ef = = 7 x 104 J (roughly 80% lost to heating up the snow).Conservation of Energy holds for conversion between all types of energy: mechanical, electrical, thermal, nuclear, chemical. On microscopic / submicroscopic levels -- these forms of energy are describable by kinetic and potential energy. E.g., energy of chemical bond consists of the motion KE, attractive and repulsive forces (therefore PE) from electrons and nuclei.
In nuclear reactions -- must take into account that mass actually can be converted to energy:
DE = Dmc^2, Einstein’s famous equation.Driver’s Training
Speed of a car increased by 50%. By what factor will minimum braking distance be increased (ignore reaction time)?
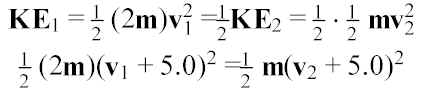
Braking force same. Therefore: Distance = 2.25 times original.
One car has 2x the mass of a second car (=m), but only half as much KE. When both cars increase their speed by 5.0 m/s they have the same KE. What were the original speeds of the cars?
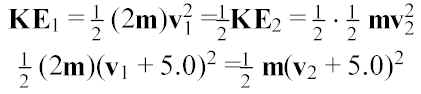
First equation: v
2 = 2v1From second equation:
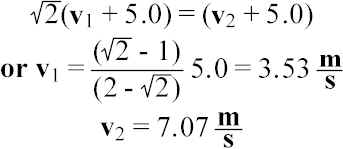
POWER
Power = rate at which work is done (or rate at which energy is transformed):
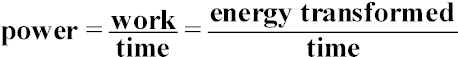
SI Units: Joule/s = 1 Watt
British: Horsepower; 1 hp = 550 ft lb/s = 746 watts.
If work is done by a constant force, F:
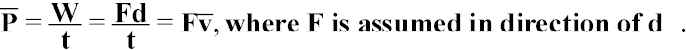
Running the
Stairs to the Stars (Physical Sciences Bldg --Basement to 14th floor); Consider POWER.1. Who could generate the highest instantaneous power?
2. Who could generate the highest average power?
What are "significant" output levels?
Person in good physical shape -- 1/10 hp (75 W) at steady pace. O
2 consumption -- 1 liter (1000 cm3)/minute.Top athlete -- (long distance sports-runners, skiers, bikers) 0.6 hp (~400 W); O
2 consumption -- 5.5 liter/minute. Gossamer: (1979) human powered airplane, piloted by world class biker, crossed English Channel -- averaged 190 W (0.3 hp).FOR approx. 1 minute spurts - 450 - 500 watts.
For fraction of a second -- several kW.
A 70 kg student runs up 2 flights of stairs (
Dh = 7.0 m) in 10 s. Compute the student’s output in doing work against gravity in(a) watts, (b) hp.
(a) W = F
Dh/t = mgDh/t = (70 kg) (9.81 m/s2) (7 m)/10s = 480 W(b) W (in hp) = W (in W)/746 = 480/746 hp = 0.64 hp
The express elevator in Sears Tower (Chicago) averages a speed of 550 m/minute in its climb to the 103rd floor ( 408.4 m) above ground. Assume a total load of 1.0 x 10
3 kg, what is the average power that the lifting motor must provide?v
avg = 550 m/minute x 1 min./60 s = 9.144 m/s.At constant v, Force to lift = F = mg;
P
avg = Fvavg = (1.0 x 103 kg)(9.144 m/s) = 89.57 kW = 90 kW.(takes ~44 s to make trip).
You want to loose weight; You therefore want to:
a)Run the stairs once/day as hard as you can, then hit the chips!, or
b) Sustain an activity that burns ~ 1CALORIE/Minute almost every day for 30-60 minutes and don’t hit the chips!
1 CALORIE = 1 Kilocalorie (4.186 kJ). 1 Kcal/minute = 70 Watts (substantial effort). To loose weight have to exercise and diet!!!
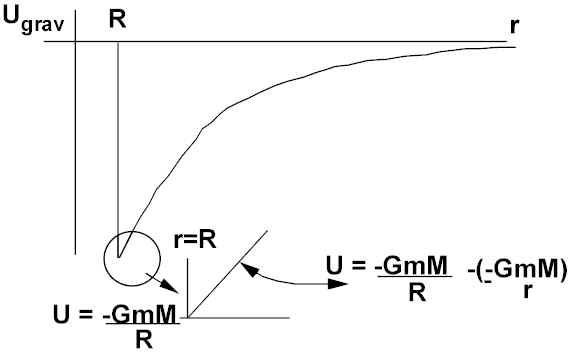
Potential Energy of the Gravitational Field
On earth’s surface, we take U = mg
Dy, where Dy (or h) is the height above the surface of the earth. This is an approximation because Fgrav depends on r (distance from center of earth). But Rearth >> Dy allows us to set Fgrav = to a constant (mg).For large distance changes, need to use 
.
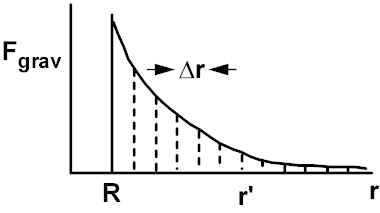
Work done in going from R to r’ = Area under curve. WITH SOME EFFORT (INTEGRATE!!) can show this to be:
The further m is from M, U becomes less negative, approaches largest value (0)
at r=infinity.
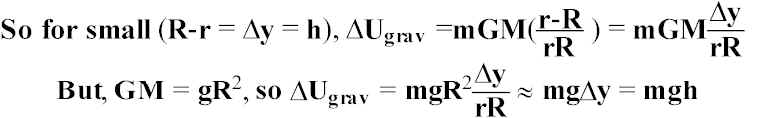
Escape Velocity
The minimum blast off speed to shoot a projectile off a planet (or moon) and never have it fall back is called the escape velocity, v
esc.
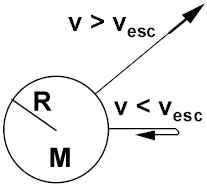
At the surface of the planet (r=R),
With no other forces except gravity of planet, Emech remains constant.
Consider projectile to arrive at r=8 with minimum KE (=0). Then E
mech = 0 + 0!!! = Initial Emech.Therefore:
